統計学の本を読みましたよ
2013年10月07日に買って以来、ずっとKindleライブラリの肥やしになっていた「ヤバい統計学」をようやく読みました。
渋滞問題やドーピング検査、宝くじの不正問題などで統計学がどのように使われているのか、がまとめられています。
ドーピング検査のエピソードでは、新型コロナウイルスのPCR検査でも話題になっている「偽陽性/偽陰性」の説明もありホットな話題でした。
1000人のアスリート(内100人が実際にドーピングをしている)に対して、95%の信頼性があるドーピング検査を実施したときの例です。
イメージ的にはこんな感じ。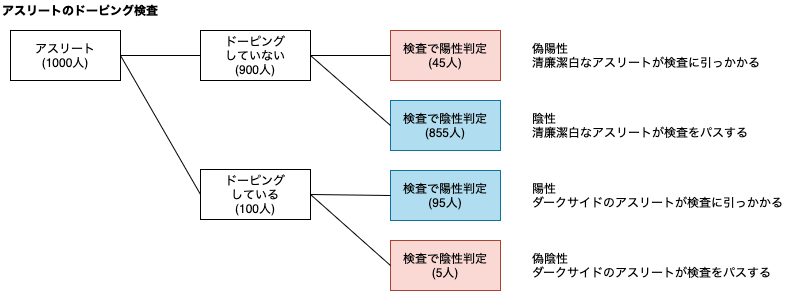
無実のアスリートの選手生命を脅かすパターン1の誤判定を減らすために検査の閾値を厳しくすると、実際にドーピングしているアスリートを見逃してしまう(パターン4)ケースが増えてしまう。
逆に、ドーピングを撲滅するために検査の閾値を下げればドーピングしている選手は見つかりやすくなりパターン4は減るが、ドーピングしていないアスリートが検査に引っかかる(パターン1)ケースが増えてしまいます。
検査が100%正確でないことを前提として、偽陽性と偽陰性をどの程度許容するのかがジレンマになります。
偽陽性/偽陰性についてはPCR検査でも同じことが言えるので、もう少し早くに読んでおきたかった項目です。
統計というと平均値や中央値といった項目がよく使われますが、「ヤバい統計学」には数値の説明は出てきませんでした。
そういった情報を知りたかったので、追加で「ニュートン式 超図解 最強に面白い!! 統計」と「Newtonライト『統計のきほん』」も読んでみました。
(重複した内容が多かったので、読むならどちらか1冊で充分ですが…)
世論調査や視聴率の実施方法や、偏差値など普段の生活でよく耳にする数値について、わかりやすく説明されています。
この内容を覚えておけば、ニュースで取り上げられる数値の見方も変わってきそうです。


